cover: Pixiv ID 141075191
三角函数
刷到飞哥的一道题。
- 求证: \sin\cos x<\cos\sin x
把柿子移到一边去,先求个导看看极值试试:
没发现有啥用,换思路。试着对外层的三角函数处理一下,用诱导公式有 \sin\cos x-\sin(\frac{\pi}{2}-\sin x)<0 ,然后和差化积: 2\cos(\frac{\cos x-\sin x}{2}+\frac{\pi}{4})\sin(\frac{\cos x+\sin x}{2}-\frac{\pi}{4})<0 。即 \sin(\frac{\sin x-\cos x}{2}+\frac{\pi}{4})\sin(\frac{\cos x+\sin x}{2}-\frac{\pi}{4})<0 ,再来就是辅助角: \sin(\frac{\sin(x-\frac{\pi}{4})}{\sqrt 2}+\frac{\pi}{4})\sin(\frac{\sin(x+\frac{\pi}{4})}{\sqrt 2}-\frac{\pi}{4})<0 ,借由 \sin 和 \cos 的周期性,只需要证明不等式在一个 2\pi 周期成立就行了,那么可知左边 \sin 里的柿子值域为 [-\frac{1}{\sqrt 2}+\frac{\pi}{4},\frac{1}{\sqrt 2}+\frac{\pi}{4}] ,右边的则是 [-\frac{1}{\sqrt 2}-\frac{\pi}{4},\frac{1}{\sqrt 2}-\frac{\pi}{4}] ,而 \frac{1}{\sqrt 2}<\frac{\pi}{4} ,两个 \sin 显然异号,不等式成立。
阿美利卡的某道简单数论
- a,b\in N^* ,a>b , \frac{1}{a}+\frac{1}{b}=\frac{2}{19} ,求 a,b .
如果是填空题,我有一无脑方法😏(其实跟瞪眼也没啥区别,只是比直接瞪更好一点
设 k\in N^* ,通个分,条件等价于 a+b=2k,\;ab=19k ,那么 a,b 就是 x^2-2kx+19k=0 的两根,用求根公式有 a=k+\sqrt{k^2-19k},b=k-\sqrt{k^2-19k} ,也就是要求 k^2-19k 是完全平方数。
这里貌似看不出啥,设 k^2-19k=t^2 ,再用个求根公式有 k=\frac{19+\sqrt{19^2+4t^2}}{2} ,这时要求 19^2+4t^2 是个完全平方数,这不就是勾股数嘛,而原生勾股数的生成式长这样: (m^2-n^2)^2+(2mn)^2=(m^2+n^2)^2 ,其中要求 m\bot n,\;m\not\equiv n \;(\bmod\; 2) ,到这已经给了很多可瞪的提示了,(2mn)^2 显然只能是 4t^2 ,而 m^2-n^2 自然是 19 ,依靠后者可以联想到 (n+1)^2-n^2=2n+1 这一奇数生成器,很显然 m=10,n=9 就能满足上述条件。这么一算 t=90,k=100 ,那么 a=190,b=10 。
但是如果是大题这个方法无法证明解的唯一性,所以又想了另一个方法。条件柿子如果能化为好看的乘积柿,或许就能质因数分解了,事实上确实可以: \frac{1}{a}+\frac{1}{b}=\frac{2}{19} 等价于 (2a-19)(2b-19)=19^2 (其实这里注意力好的话也能联想到刚才的奇数生成器,只是提示相对前一种方法没那么足),很容易发现 2a-19 和 2b-19 都要 >0 ,那么 19^2 也就两种分配方案 19\times19 和 1\times 19^2 ,因为 a>b ,所以 2a-19=19^2,2b-19=1 ,解出 a=190,b=10 ,做完了。
唐人压轴
刷 b 站看到的,这还压轴?
- 原题: \sin x+\sin 2x+\sin 3x=\cos x+\cos 2x+\cos 3x=0 ,求 \cos 2x .
和差化积: (2\cos x+1)\sin 2x=(2\cos x+1)\cos 2x=0 ,\cos x=-\frac{1}{2} ,\cos 2x=-\frac{1}{2} ,做完了。
加强一下:\sum_{i=1}^n \sin ix=\sum_{i=1}^n \cos ix=0 ,求 x 的解集。
这个容易看出来就是 \frac{2k\pi}{n} ,但是如何严谨的证明?注意到:
有 \sin nx=0 ,同理 \cos nx=0 , 可知 x\in \{\frac{2k\pi}{n}|k\in Z\} 。
局部不等式分析
- a,b,c,d>0,abcd=1 ,求证: \frac{1}{(1+a)^2}+\frac{1}{(1+b)^2}+\frac{1}{(1+c)^2}+\frac{1}{(1+d)^2}\geq 1 .
刚开始的时候换了个元,变化后的等式条件并没有很好看。考虑从取等条件入手,显然可猜出来 a=b=c=d=1 时柿子取到 1 ,对这个条件构造不等式的话貌似有三个大方向:
- 利用相等的性质,构造类基本不等式状物
- 利用 =1 的性质,更为灵活
- 两个都用
我先尝试了第一种,很不幸,由于平方里带常数的形式,怎么构造也造不出来,索性就放弃了。转第二种,常数的威力主要集中在乘法上,想起来这种分式有一种将分母里的某个加数删去的放缩法,于是将平方拆开来看看: \frac{1}{a^2+2a+1} ,接下来真就是凭感觉和经验乱试了,貌似我运气比较好,蒙中了一个不等式: \frac{1}{a^2+2a+1}= \frac{b}{a^2b+2ab+b}\geq \frac{b}{a^2b+ab^2+a+b}=\frac{b}{(a+b)(1+ab)} ,这个形式刚好可以两两配个对,即
c,d 同理是 \frac{1}{1+cd},同时也是 \frac{1}{1+\frac{1}{ab}} ,两式通分一加就是原结论。
其实个人感觉这种题没有一定的经验第一次根本做不出来,我能蒙出 std 真的纯属侥幸。
但是闲着也是闲着,于是又去网上找了相关局部不等式的相关信息学习了一下,发现了一种出现频率比较高的放缩 trick ,在此记录一下:
假设 f(x)\leq Ax+B ,然后待定系数求 A,B ,常用于证明轮换不等式。
期望之比
在油管上看到一个非常有意思的东西,大概意思是说有一个圆,在圆内均匀随机点三个点,保证三点不共线,如下图:
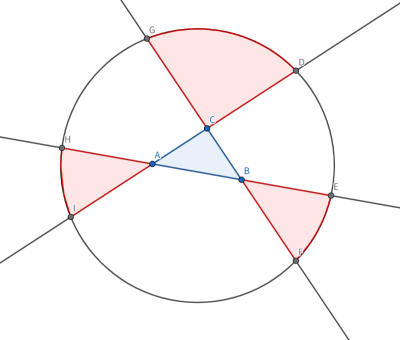
A,B,C 就是随机点的三个点,求图中红色面积的期望与蓝色面积的期望之比。
图形十分不规则,如果常规建系肯定不好做,于是看了半天还是没思路,又倒回视频开头重新看了一遍题目描述,其中对于均匀随机的解释中的一句话给了我 hint :
まず、「偏りなく無作為に点を打つ」といったが,正確には、円の面積を1として、円の内部の面積Sの任意の領域に対して、点がその領域に入る確率がSになるように打つ
神秘机翻: 就是如果设圆的面积为 1 ,那么在圆内随机点一个点在圆内某个面积为 S 的区域内的概率就是 S 。
粗略写一下期望比的柿子:
S_R 就可以视作另一个随机点在红色区域的概率,那么 \displaystyle\sum_{S_R} S_R\cdot p(S_R) 就能视作一个新点点在红区的概率,S_B 同理,问题就转化为了按顺序点四个点,求最后一个点在红区的概率比在蓝区的概率。
到这里就容易考虑了,考虑任意四个点,而这四个点的任意顺序都是等概率的,进而有每个点作为第四个点也是等概率的,所以只对任意的四点单独考虑,发现有凸四边形和凹四边形两种情况:
- 凸四边形:
考虑每个点作为最后一个点,发现全部既不在红区也不在蓝区,对答案无影响。
- 凹四边形:
考虑每个点作为最后一个点,发现仅有一个点在蓝区,剩下三个点都在红区,可得出概率比是 3 。
综合一下,\frac{E[Red]}{E[Blue]}=3 。这个结果与圆形无关。
然而视频后面又跟了一问,假设圆半径为 r ,求 E[Blue] .
没想到啥方法,设极坐标系下三个点坐标为 (i,x),(j,y),(k,z) ,那么 S_B=\frac{1}{2}|\sum\limits_{cyc}xy\sin(j-i)| ,直接枚举:
设算子 \mathop {S_x}\limits^u f(x) 表示 \displaystyle\int_0^{u}f(x)dx
(为了做这个积分被迫学了一堆技巧 qwq

