“n 阶 0-t 数列”
若 n 项数列 \{a_n\} 同时满足 \sum_{i=1}^{n}a_i=0 \;,\sum_{i=1}^{n}|a_i|=t ，则称 \{a_i\} 为 “n 阶 0-t 数列” 。
- (1) 若等比数列 \{a_i\} 为 “6 阶 0-1 数列”，写出各项。
- (2) 若等差数列 \{a_n\} 为 “2k-1 阶 0-t 数列” (k\geq2 且 k \in N^* ， t\in N^* ) ，求 a_n （用 k,n,t 表示)。
- (3) \{a_i\} 为 “n 阶 0-t 数列” ，记 s 为其前缀和且满足 \exists \; m\in [1,n] ,s_m=\frac{t}{2} ，求证： \{s_n\} 不是 “n 阶 0-t 数列” 。
(1)
容易构造
1,-1,1,-1,1,-1,1,-1
语：就算是 T19 (1) 出这么简单真的好吗。
update on 2026.1.24 22:48:11.4514 ：答案是 \frac{1}{6},-\frac{1}{6},\frac{1}{6},-\frac{1}{6},\frac{1}{6},-\frac{1}{6} ，作者码字时路昏了。
就算是 T19 (1) 出这么简单真的好吗。
(2)
设 a_n=pn+b ，那么：
由 (1) ：
因为 k\in N^* ，所以 b=-pk ，代入 (2) 得：
所以 a_n=\pm \frac{t}{k(k-1)}n \mp \frac{t}{k-1}
语：超级喜欢这种带 \Sigma 狂推柿子的题。推柿子，爽！（解几敬谢不敏
(3)
为了方便记 s_0=0
题意转成这样：
数列 \{s_n\} 满足
求证 \{s_n\} 不同时满足
证明：假设能同时满足。
考虑绝对值不等式 \sum_{i=1}^{n}|x_i|\geq |\sum_{i=1}^n x_i| 对 (3) 放缩：
等号成立当且仅当 s_1\leq s_2\leq \dots \leq s_n 或 s_1\geq s_2\geq \dots \geq s_n
因为 t=t 是一个恒等式，所以 s_1\leq s_2\leq \dots \leq s_n 或 s_1\geq s_2\geq \dots \geq s_n，又由于 s_m=\frac{t}{2}\geq 0=s_n，故 s_1\geq s_2\geq \dots \geq s_n
结合 (5) 知：s_1=\frac{t}{2} ，由 (4) ：\sum_{i=2}^{n}s_i=-\frac{t}{2} < 0 ，与 s_2\geq \dots \geq s_n=0 矛盾，故命题不成立。
语：总感觉哪里的逻辑有漏洞，好像是 “同时满足” 和反证法的结合那一块。std 貌似是把绝对值不等式证了一遍。
折射率到底偏大还是偏小
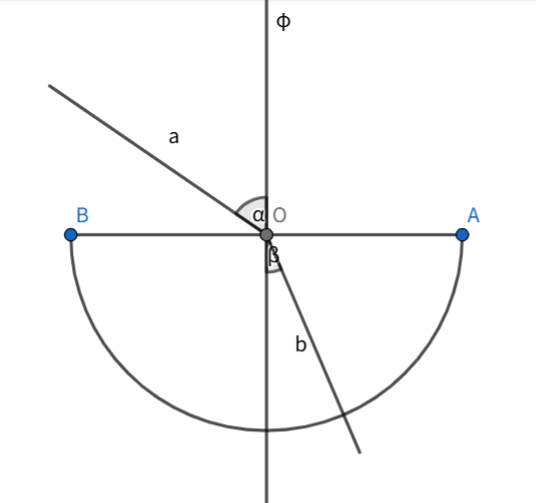
如图， a 是入射光线， b 是经过半圆形玻璃砖折射后的折射光线，\Phi 是法线，然后原题有说用这个测折射率，不小心碰了一下云云，最后问题可以变成：将玻璃砖逆旋一个小角 \theta ，其他不变，新的折射光线 b' 在 b 上方还是下方？
“标准答案” 犯了没考虑旋转本身带来的偏移的错误（它认为是在下方，我认为在上方，然后我折腾一中午想我错在哪了结果发现原来 tm 是答案错了
来证明一下：
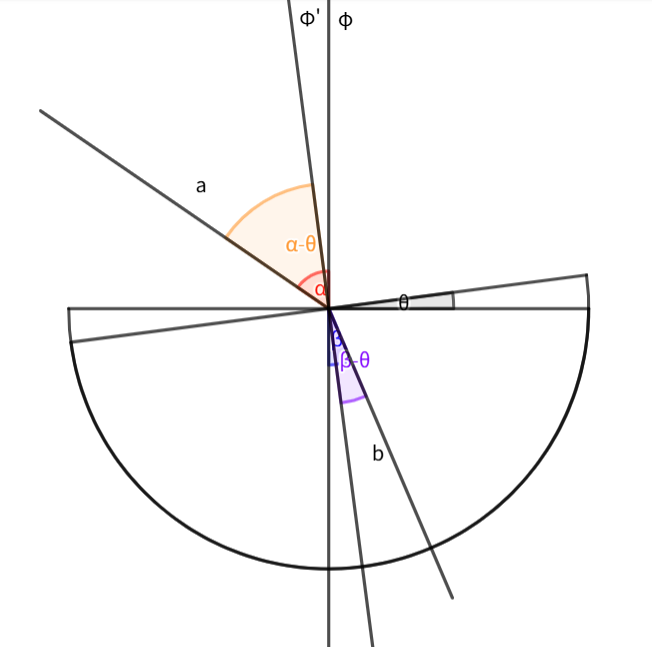
设旋转后的新法线为 \Phi ' ，a 和 \Phi ' 入射角 \alpha - \theta 对应的折射角为 \gamma ，即证：\sin \gamma > \sin (\beta-\theta)
考虑对所证不等式进行变形：
由折射定律：
若 \alpha-\beta-\theta>0 ，由 \theta>0 不等式成立；反之，由 \alpha>\beta 不等式同样成立。