快回老家了,闲来无事遇到了一些有趣的小问题,作为活跃思维的小菜还是挺好的。
\pi^e 和 e^\pi 谁大?
这题是和同学讲批话时想到的。
主要体现了一个统一形式的想法,先说结论 e^\pi> \pi^e ,下面证明它。
即证:e^{\frac{1}{e}}>\pi^{\frac{1}{\pi}}
分析一下增减性:对 x^{\frac{1}{x}} 求导得 x^{\frac{1}{x}}\frac{1-\ln x}{x^2} ,求一下极值点发现也就 x=e 的时候行,再求个二阶导发现这是极大值,结论得证。
求 3^{2026} 十进制下的后四位
在 b 站上刷到的,看视频的做法是一个二项式蜜汁展开,评论区里全是快速幂硬算和“注意到”,其实结合一点数论可以很快得到一个好想且手算也简单的做法。
由欧拉定理:3^{\varphi(10^4)} \equiv 3^{10^4\cdot (1-\frac{1}{2})(1-\frac{1}{5})}\equiv 3^{4000}\equiv 1 \;(\bmod \;10^4)
故 3^{2000}\equiv 1 或 -1\;(\bmod \;10^4)
同样由欧拉定理:3^4\equiv 1\;(\bmod \;10) 可知 3^{2000}\equiv 1\;(\bmod \;10)
那么 3^{2000}\equiv 1\;(\bmod \;10^4)
接下来只需用手动快速幂计算 3^{26}\equiv 9^{13}\equiv 81^{6}\cdot 9\equiv 6561^{3}\cdot9 \equiv 8329\;(\bmod \;10^4)
嵌套
- f(f(x))=x^2-x+1 ,求 f(0)
先把 x=0 代一发再说: f(f(0))=1
然后看到这种嵌套就手痒求了个不动点,x=1 ,此时 f(x)=1 或 0
当 f(1)=0 时:再套一层 f ,f(f(f(0)))=0=f^2(0)-f(0)+1 , f(0) 无解。
当 f(1)=1 时:f(f(f(0)))=1=f^2(0)-f(0)+1 ,得 f(0)=0 或 1 。又因为 f(f(0))=1 可知 f(0)=1 。
幂塔方程引发的小思考
起因是随机跳到一道黑,显然我不会做(
但是对这个幂塔起了兴趣:
先对重幂下个定义:
那么原问题就是求解方程 \lim_{n\rightarrow \infty} {^n}x=2 。
看似可以用比较初等的方法得出解(不知道严谨性如何):
原方程等价于 \lim_{n\rightarrow \infty} {^n}x=x^{\lim_{n\rightarrow \infty} {^n}x}=x^2=2 ,解得 x=\sqrt 2 。
这里同时也能看出数列 \{{^n}[\sqrt 2]\} 是收敛的,然后我就开始好奇在收敛的前提下 x 最大能是多少呢,毕竟像 \{{^n}2\} 的话就是发散的。
设 \lim_{n\rightarrow \infty} {^n}x=x_0 (其实 x_0 也是数列 \{{^n}x\} 的不动点),如法炮制可得 x^{x_0}=x_0 ,也就是要求方程 a^x=x 有恰有一个解,此时的 a 就是所求的最大值。
其实就是找到一个底数最大的指数函数与直线 y=x 相切。
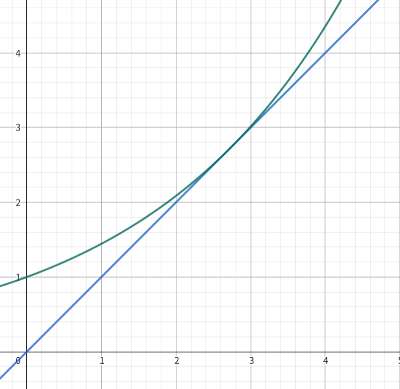
这个其实也很好找,设切点为 (x_0,a^{x_0}) ,求个导有 a^{x_0}\ln a=1 ,即 x_0=-\frac{\ln\ln a}{\ln a} ,那么切点就是 (-\frac{\ln\ln a}{\ln a},\frac{1}{\ln a}) ,又因为 y=x 过 (0,0) ,所以 \frac{\frac{1}{\ln a}-0}{-\frac{\ln\ln a}{\ln a}-0}=1 ,解出 a=e^{\frac{1}{e}} 。
嗯? e^{\frac{1}{e}} 看上去有点熟悉?貌似比 \pi^{\frac{1}{\pi}} 大来着?同时还是 x^{\frac{1}{x}} 的最大值来着?
其次分式
出现在神人自造的 gal 选项里(依旧 b 站刷到的),题本身没啥意思。
- a>b>0 , 求 [\frac{a^2+b^2}{ab-b^2}]_{\min} .
其次啊,那就只关注 a,b 的相对大小的影响,设 x=\frac{b}{a} ,那 x \in (0,1) ,那原式就是 \frac{x+x^{-1}}{1-x} ,随便化简得 -1-\frac{1}{x+1+\frac{2}{x+1}-3} \geq 2+\sqrt 2
神秘求极值
- x^2+y^2+xy=1 ,求 [2x^2+y^2]_{\max}
长这种的,一般都先考虑做一些蜜汁换元把条件等式搞得简单一点,这里的条件里有个难看的 xy ,考虑把它搞掉。随便配一下有 \frac{3}{4}x^2+(y+\frac{1}{2}x)^2=1 ,然后就能三角换元: x=\frac{2}{\sqrt 3}\sin t , y=\cos t-\frac{1}{\sqrt 3}\sin t ,这样一来,极值就很好求了:
其实第一眼看到 xy 还有另一条路, xy 可以跟旋转或是平方差扯上关系,所以 x^2+y^2+xy=1 长的就像一个旋转的椭圆(虽然后续做法用不上椭圆的性质),一般情况下直接待定系数求旋转系数还挺麻烦的,但是这个柿子这么对称一看就知道旋转 \frac{\pi}{4} 肯定没毛病,那么令 x\leftarrow \frac{x-y}{\sqrt 2},\;y\leftarrow \frac{x+y}{\sqrt 2} ,原问题变成:\frac{x^2}{2}+\frac{3y^2}{2}=1 ,求 [\frac{3}{2}(x^2+y^2)+xy]_{\max}
直接把 \frac{x^2}{2}+\frac{3y^2}{2}=1 除到 \frac{3}{2}(x^2+y^2)+xy 分母上,有 \frac{3}{2}(x^2+y^2)+xy=\frac{\frac{3}{2}(x^2+y^2)+xy}{\frac{x^2}{2}+\frac{3y^2}{2}} ,分子分母其次,用处理其次分式的套路就行。

