代码实现和一些思路参考了一些题解。
遇到这种序列上研究大小的序列问题,应该主动考虑笛卡尔树。
对原序列建出一棵大根笛卡尔树。稍微转化一下问题的连边条件,首先每个节点必定和它的左子树同在所有点在同一个连通块,这样初步连边后可以看出连通块与连通块之间通过树上右链(从根一直向右走的链)的边进行连接,大概长这样:
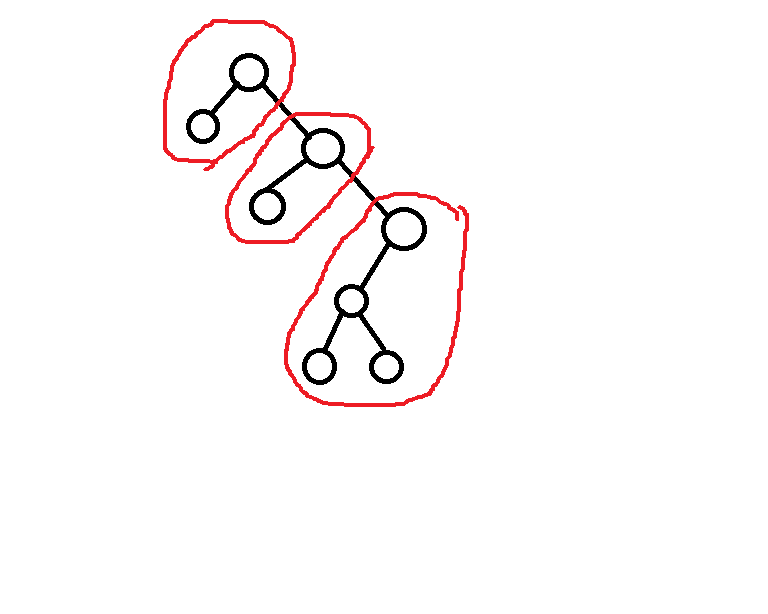
其次还可能有一些连向右子树的边,而这些边连上后肯定只会使右链上相邻的若干个块合并,简单证一下:设 x,y,z 为右链上的三个节点, x 是 y 祖先, y 是 z 祖先,x,z 合并了而 y 没有,根据连边条件,那么 x 块中一定有一个节点值比 z 小,由笛卡尔树性质, y 又比 z 大,所以 y 一定能向 x 连边合并,所以 x 到 z 之间的所有块都能和 x,z 合并。
有了这个性质,统计连通块就可以变为统计右链上点满足其值小于树中出除去它的子树以外部分最小值(也就是连通块在右链上左端点)的个数,把上面结论所有推回序列上就是统计这么一个值 v 的个数:若把大于 v 的值看成 1 ,小于等于 v 的值看成 0 ,则原序列变为形如 111..11000..00 。
于是就可以对每个 v 维护 10 相邻对数的个数,若个数为 1 就是一个合法的 v 。而对于序列上相邻两个数 a_i,a_{i+1} ,它就会对 [\min(a_i,a_{i+1}),\max(a_i,a_{i+1})) 产生 1 的贡献。为了方便设 a_0 为极大值, a_{n+1} 为极小值,这样就可以用线段树维护最小值和最小值的个数。
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10,M=1e6+10;
int n,q;
int a[N];
struct st{
struct node{
int l,r,m;
int sum,v;
int add;
}d[M<<2|1];
void pushup(int p){
int l=p<<1,r=l|1;
d[p].v=min(d[l].v,d[r].v);
d[p].sum=0;
if(d[p].v==d[l].v)d[p].sum+=d[l].sum;
if(d[p].v==d[r].v)d[p].sum+=d[r].sum;
}
void pushdown(int p){
int l=p<<1,r=l|1;
if(d[p].add){
d[l].add+=d[p].add;
d[r].add+=d[p].add;
d[l].v+=d[p].add;
d[r].v+=d[p].add;
d[p].add=0;
}
}
void build(int p,int l,int r){
d[p]=(node){l,r,l+r>>1,0,M,0};
if(l==r)return ;
build(p<<1,l,d[p].m);
build(p<<1|1,d[p].m+1,r);
pushup(p);
}
void add(int p,int l,int r,int k){
if(l<=d[p].l&&d[p].r<=r){
d[p].v+=k;
d[p].add+=k;
return ;
}
pushdown(p);
if(l<=d[p].m)add(p<<1,l,r,k);
if(r>d[p].m)add(p<<1|1,l,r,k);
pushup(p);
}
void modify(int p,int x,int k){
if(d[p].l==d[p].r){
if(k)d[p].sum=1,d[p].v=d[p].add;
else d[p].sum=0,d[p].v=M;
return ;
}
pushdown(p);
if(x<=d[p].m)modify(p<<1,x,k);
else modify(p<<1|1,x,k);
pushup(p);
}
}t;
void work(int i,int k){
int l=min(a[i],a[i+1]),r=max(a[i],a[i+1]);
t.add(1,l,r-1,k);
}
void opt(int pos,int x){
work(pos-1,-1),work(pos,-1);
t.modify(1,a[pos],0);
a[pos]=x;
work(pos-1,1),work(pos,1);
t.modify(1,x,1);
}
int main(){
scanf("%d%d",&n,&q);
t.build(1,0,M);
a[0]=M-5,a[n+1]=0;
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
t.modify(1,a[i],1);
}
for(int i=0;i<=n;++i)work(i,1);
while(q--){
int pos,x;
scanf("%d%d",&pos,&x);
opt(pos,x);
if(t.d[1].v==1)
printf("%d\n",t.d[1].sum);
else printf("0\n");
}
return 0;
}
第一次写题解,感觉把想法化为语言好困难啊,如有不足请指出。

