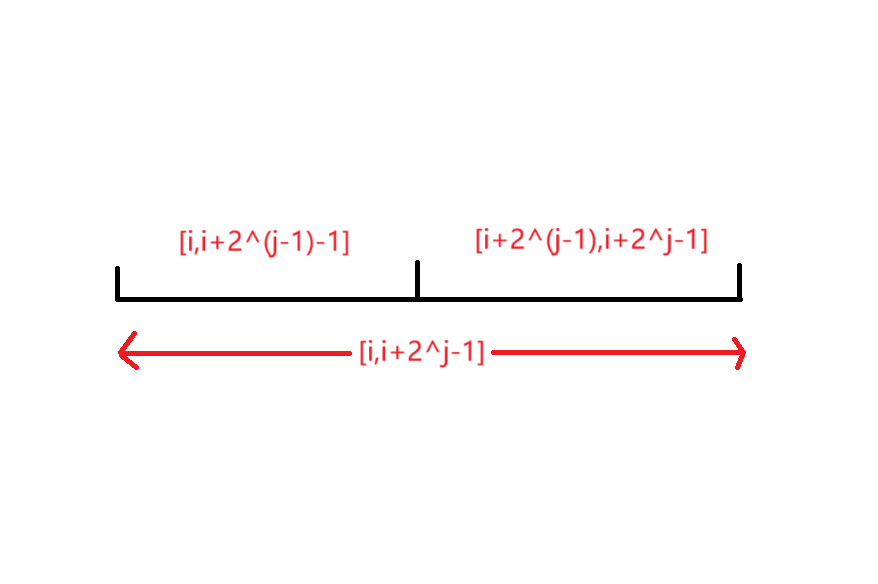线段树真的是一种挺折磨人的数据结构，但它的应用范围也是非常广泛的。它可以在 $O(\log n)$ 的时间内完成区间修改和区间查询。似乎有句话是这么说的：树状数组能做的，线段树都能做；线段树能做的，树状数组不一定能做。

线段树的操作

线段树是一种二叉树，它的每一个节点都代表了一个区间。对于一个区间 $[l, r]$，它的左儿子代表了 $[l, mid]$，右儿子代表了 $[mid+1, r]$。其中 $mid = \frac{l+r}{2}$。

依然以区间和为例。

建立

通常来说线段树的建立是以递归进行的，由于后面会涉及到区间修改等操作，所以我通常用一个结构体来存储线段树的信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct{
	LLI l,r,sum;
}d[4*N];//4倍空间，不然存不下

void build(LLI l,LLI r,LLI p){
	d[p].l=l,d[p].r=r;
	if(l==r){//直接存储数值
		d[p].sum=a[l];
		return;
	}
	LLI m=l+((r-l)>>1);
	build(l,m,p*2),build(m+1,r,p*2+1);
	d[p].sum=(d[p*2].sum+d[p*2+1].sum);
}

查询

对于区间查询，如果当前不为所查区间的子区间，递归查询有交集的左右儿子即可。若当前区间完全包含所查区间，则直接返回当前区间的和。

1
2
3
4
5
6
7
8
LLI query(LLI l,LLI r,LLI p){
    if(d[p].l>=l&&d[p].r<=r)return d[p].sum;
    LLI m=d[p].l+((d[p].r-d[p].l)>>1);
    LLI ans=0;
    if(l<=m)ans+=query(l,r,p*2);//左儿子有交集
    if(r>m)ans+=query(l,r,p*2+1);//右儿子有交集
    return ans;
}

修改

前面两个操作都不难理解，但区间修改就有点麻烦了。首先要引入一个叫懒标记的东西，但我们修改线段树时，并不会立即修改所有的节点，而是先在所修改区间包含的每个最大子区间打上懒标记，在需要查询的时候再修改。这样就可以保证修改的时间复杂度是 $O(\log n)$ 的。

这里还涉及到了一个操作，就是将懒标记下传(pushdown)。在查询或修改的时候，如果当前节点有懒标记，但这个节点包含的区间并非目标区间的子区间，这时就将懒标记下传给左右儿子。

以区间加为例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
struct{
	LLI l,r,sum,add/*懒标记*/;
}d[4*N];

void pushdown(LLI p){
	LLI l=p*2,r=l+1;
	d[l].sum+=(d[l].r-d[l].l+1)*d[p].add;
	d[r].sum+=(d[r].r-d[r].l+1)*d[p].add;
	
	d[l].add+=d[p].add;
	d[r].add+=d[p].add;
	
	d[p].add=0;
}

void add(LLI l,LLI r,LLI p,LLI k){
	if(l<=d[p].l&&r>=d[p].r){//当前节点包含的区间是目标区间的子区间
		d[p].add=(d[p].add+k);
		d[p].sum=(d[p].sum+k*(d[p].r-d[p].l+1));
		return;
	}
	pushdown(p);//懒标记下传
	LLI m=d[p].l+((d[p].r-d[p].l)>>1);
	if(l<=m)add(l,r,p*2,k);
	if(r>m)add(l,r,p*2+1,k);
	d[p].sum=(d[p*2].sum+d[p*2+1].sum);
}

LLI query(LLI l,LLI r,LLI p){
    if(d[p].l>=l&&d[p].r<=r)return d[p].sum;
    pushdown(p);
    LLI m=d[p].l+((d[p].r-d[p].l)>>1);
    LLI ans=0;
    if(l<=m)ans+=query(l,r,p*2);
    if(r>m)ans+=query(l,r,p*2+1);
    return ans;
}

线段树维护的优先级问题

在实际应用中，线段树的维护可能会涉及到多个操作，比如区间加、区间乘、区间赋值等。这时就需要考虐到这些操作的优先级问题。比如区间加和区间乘，如果先加后乘和先乘后加的结果是不一样的。此时的应对方法一般是引入多个懒标记，每个懒标记对应一个操作，然后在 pushdown 的时候按照优先级依次下传。

以区间加和区间乘为例。先看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
struct{
	LLI l,r,sum,mul,add;
}d[4*N];

void pushdown(LLI p){
	LLI l=p*2,r=l+1;
    //part1
	d[l].sum=d[p].mul*d[l].sum+(d[l].r-d[l].l+1)*d[p].add;
	d[r].sum=d[p].mul*d[r].sum+(d[r].r-d[r].l+1)*d[p].add;
	//part2
	d[l].mul=d[p].mul*d[l].mul;
	d[r].mul=d[p].mul*d[r].mul;
	//part3
	d[l].add=d[l].add*d[p].mul+d[p].add;
	d[r].add=d[r].add*d[p].mul+d[p].add;
	
	d[p].mul=1,d[p].add=0;
}

可以看出，首先pushdown了乘法标记，然后pushdown了加法标记。这样就保证了先乘后加的优先级。

接下来更直观的了解一下这样做的正确性。假设我们有一个区间 $[l, r]$，设其和为$s$，我们先加 $k$，再乘 $p$。那么这个区间的和就是 $(s+k)p=sp+kp$。而如果我们先乘 $p$，再加 $k$，那么这个区间的和就是 $sp+k$。可以看出，两者是不一样的。

当然为此add和mul操作也要做相应的修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void add(LLI l,LLI r,LLI p,LLI k){
	if(l<=d[p].l&&r>=d[p].r){
		d[p].add=d[p].add+k;
		d[p].sum=d[p].sum+k*(d[p].r-d[p].l+1);//加法直接加就行
		return;
	}
	pushdown(p);

	LLI m=d[p].l+((d[p].r-d[p].l)>>1);
	if(l<=m)add(l,r,p*2,k);
	if(r>m)add(l,r,p*2+1,k);
	d[p].sum=d[p*2].sum+d[p*2+1].sum;
}
void mul(LLI l,LLI r,LLI p,LLI k){
	if(l<=d[p].l&&r>=d[p].r){
        //乘法要乘到add和sum上，这样才能保证pushdown的正确性
		d[p].add=d[p].add*k;
		d[p].mul=d[p].mul*k;
		d[p].sum=d[p].sum*k;
		return;
	}
	pushdown(p);

	LLI m=d[p].l+((d[p].r-d[p].l)>>1);
	if(l<=m)mul(l,r,p*2,k);
	if(r>m)mul(l,r,p*2+1,k);
	d[p].sum=d[p*2].sum+d[p*2+1].sum;
}