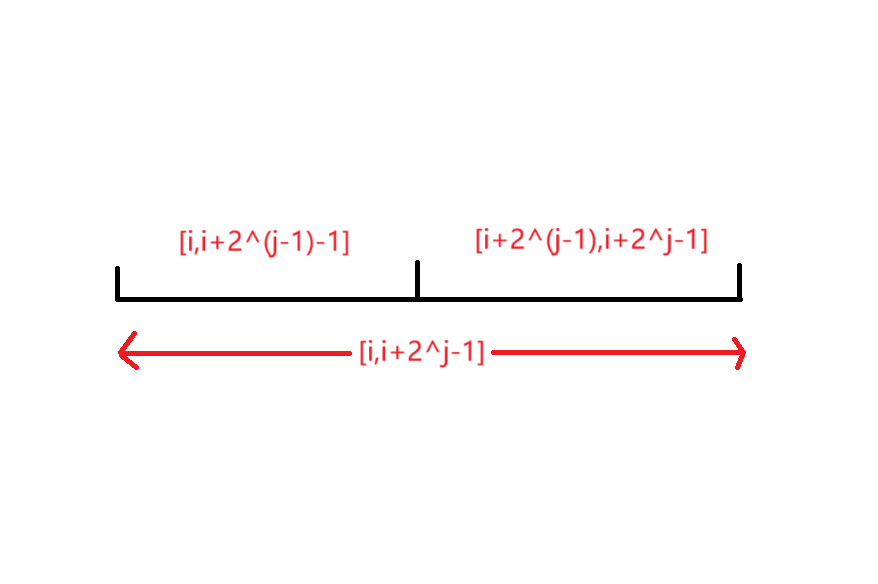二十天左右的集训结束了，虽然学校的教学完全学不到任何东西，但得承认通过自学学到了不少东西。

自学的第一个知识就是树状数组，它可以在 $O(\log n)$ 的时间内完成单点修改和前缀和查询。由于码量奇少，在搭配上差分数组和权值数组，就能实现许多骚操作。

树状数组的结构

以下以维护区间和为例。假设使用$c[i]$数组作为树状数组，它存储了原数组的某一段区间和。右端点是 $i$，左端点是 $i - lowbit(i) + 1$，其中 $lowbit(i)$ 是 $i$ 的二进制表示中最低位的 $1$ 的位置。比方说 $6 = (110)_2$，那么 $lowbit(6) = 2 = (10)_2$。

在树状数组中，每一个 $c[i]$ 都指向父亲 $c[i+lowbit(i)]$。在区间和的情况下，$c[i]$ 存储了 $[i-lowbit(i)+1, i]$ 的区间和。比如 $c[4]$ 存储了 $[1, 4]$ 的区间和。如下图所示：
树状数组

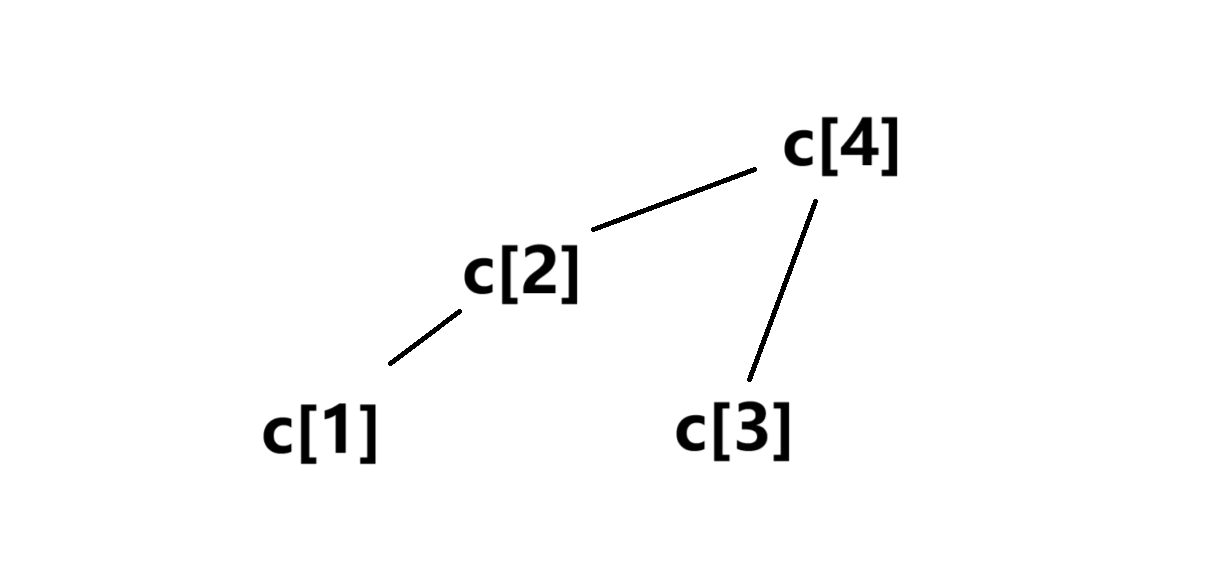
其中每一层$c[i]$都等于它的子节点之和与原数组以$i$为下标的数值之和，即$c[i] = a[i]+\sum_{j=i-lowbit(i)+1}^{i}c[j]$。

摸清楚结构后，树状数组的单点修改和前缀和查询就非常好写了。对于单点修改，只需自底向上更新父节点即可。对于前缀和查询则反过来自顶向下累加即可。

树状数组的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int lowbit(int x){
	return x&-x;
}
int getsum(int x){
	int ans=0;
	while(x>0){
		ans+=c[x];
		x=x-lowbit(x);
	}return ans;
}
void add(int x,int k){
	while(x<=n){
		c[x]+=k;
		x+=lowbit(x);
	}
}

树状数组的其他应用

区间加

如果题目要求实现这么个操作：给定一个区间 $[l, r]$，使得 $a[l], a[l+1], \cdots, a[r]$ 都加上 $k$。这时候就可以使用差分数组和树状数组来实现。

差分数组是指原数组的相邻两个元素之差，即 $d[i] = a[i] - a[i-1]$。这时，可以以$d[i]$为原数组建立树状数组，然后对于区间 $[l, r]$，只需在 $d[l]$ 加上 $k$，在 $d[r+1]$ 减去 $k$ 即可。这样就将区间加的操作转化为了单点加。

1
2
3
4
void f(int l,int r,int k){
    add(l,k);
    add(r+1,-k);
}

接下来是查询的问题，由$d[i]=a[i]-a[i-1]$可得$a[i]=d[i]+d[i-1]+d[i-2]+\cdots+d[1]$，所以只需求出$d[1],d[2],\cdots,d[i]$的前缀和即可得到$a[1],a[2],\cdots,a[i]$。

但这样只能求出某一个$a[i]$，如果要求$a[l…r]$的和，那么一个一个求时间上会很慢。甚至不如不用树状数组，这时候就需要维护第二个树状数组$d[i]*i$，原因请看公式：

我们知道

所以

可见要求出$a[l…r]$的和，只需求出$\sum{i=l}^{r}d[i]$和$\sum{i=l}^{r}id[i]$即可。因此，我们需要维护两个树状数组，一个维护$d[i]$的前缀和，一个维护$d[i]*i$的前缀和。